はじめに
画像認識関連の開発や調査をしているとカルマンフィルタに出くわす事がありますが、よくわかっていない部分があったので改めて勉強することにしました。
前半は勉強したことのまとめ、後半は具体的な数値シミュレーション例を記載します。
カルマンフィルタとは
概要
- 観測値からシステムの状態を推定するアルゴリズム。逐次ベイズフィルタの一種。
- 1960年代にカルマン(Rudolf Emil Kalman)によって提案され、アポロ計画において人工衛星の軌道推定に使われたことで有名になった。
- 現在でも、航空・宇宙工学、ロボット工学、画像処理、計量経済学、生物学といった幅広い分野においてカルマンフィルタおよびそれを拡張したアルゴリズムが活用されている。
処理の流れ
以下にカルマンフィルタを利用する流れを簡単にまとめます。
1. 対象とする時系列システムのモデリング
一般にカルマンフィルタでは「状態空間モデル」を用いて状態を推定します。
※状態空間モデル:測定などで直接得られる「観測値」と、直接得られない潜在的な「状態」を設定するモデル
ここでは、以下のような離散時間の状態空間モデルを考えます。
1つ目の式はある時刻の状態から次の状態を求める式であり、「状態方程式」とも呼ばれます。
2つ目の式は状態から観測値を得る式であり、「観測方程式」とも呼ばれます。
はシステムノイズと呼ばれ、平均0, 分散
の正規白色ノイズ、
は観測ノイズと呼ばれ、平均0, 分散
の正規白色ノイズです。
また、は既知の係数行列・ベクトルであり時間的に一定とします。
2. カルマンフィルタによる状態推定
上で設定した状態空間モデルに対し、カルマンフィルタで状態推定を行うステップを以下に記載します。 ※真の状態に対し、状態の推定値は
で表します。
(1) 予測ステップ
予測ステップでは事前状態推定値と事前誤差共分散行列を求めます。
※上付きのマイナス記号は"事前"であることを示しています。
(2) フィルタリングステップ
フィルタリングステップではまず「カルマンゲイン」を計算し、これを用いて状態推定値と誤差共分散行列を更新します。
※カルマンゲインは予測ステップで求めた予測値に対し、"観測"による補正をどれだけ入れるかをコントロールする役割。
以上のように、「予測」と「フィルタリング」から成る一連の更新式を、観測値を受け取る度に逐次的に実行していくのがカルマンフィルタの特徴です。
簡単な具体例
ここでは以下のシステムを考えます。
これは前述の状態空間モデルにおいて状態xをスカラーとし、A=b=c=1とおいたものです。
この場合、カルマンフィルタによる推定のステップは以下となります。
(1) 予測ステップ
(2) フィルタリングステップ
この例で、実際にシミュレーションを行ってみます。
以下は参考文献のMATLABコードを少し変更してpythonで書いた物です。
実行結果を以下に示します。
青が真の状態、グレーが観測値、赤がカルマンフィルタによる状態の推定値です。
・の場合
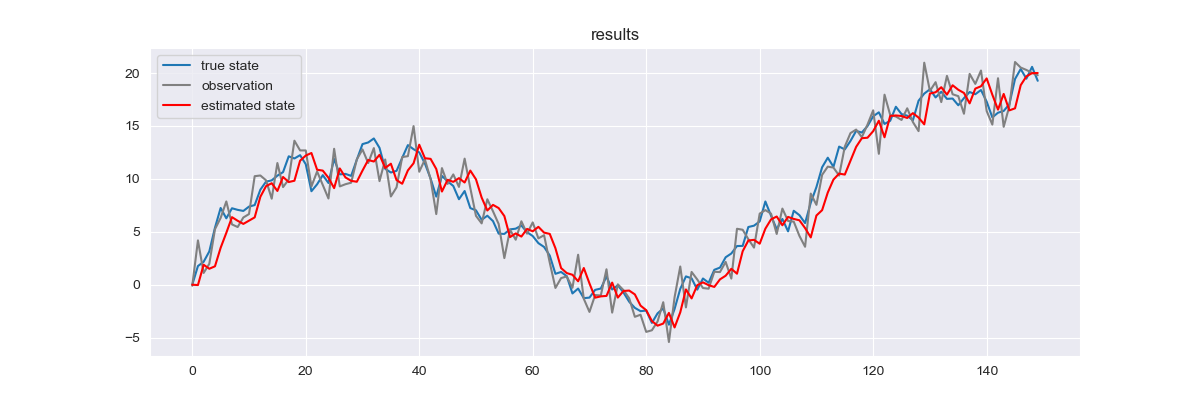
・の場合
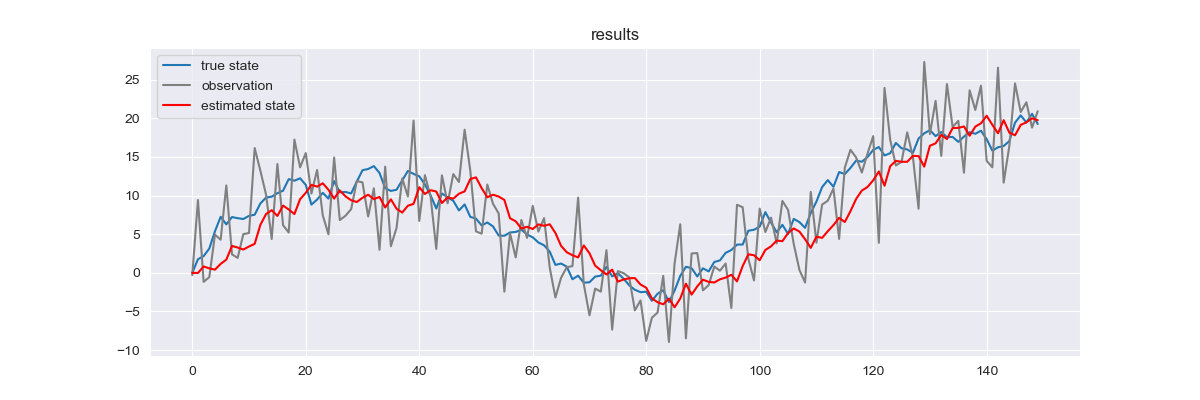
観測ノイズを大きくした場合でも、カルマンフィルタによって真の状態に近い値が推定できていることがわかります。
今回の記事は以上です。
参考
- 『カルマンフィルタの基礎』